อาร์คิมีดิส

กาลครั้งหนึ่ง นานมาแล้วบนแผ่นดินเซอราคิวส์ ที่ตั้งของประเทศกรีซใน ปัจจุบัน นักคณิตศาสตร์ผู้ปราดเปรื่องท่านหนึ่งได้คิดทฤษฎีว่าด้วยรูปทรง ปริมาตร ดวงดาว และกลศาสตร์ ต่างๆ มากมาย เวลาที่ผ่านเนิ่นนานมา ค่อยๆ ย่อยทำลายประวัติอันน่าสนใจของท่านจนเหลือเพียงเรื่องราวของ นักวิทยาศาสตร์สติเฟื่องที่ร้อง “ยูเรก้า” แล้ววิ่งแจ้นมาจากโรงอาบน้ำ เพื่อพิสูจน์มงกุฎทองคำของพระราชา

ใครๆ คงรู้จักชื่อของอาร์คิมีดิสดี นักคณิตศาสตร์ท่านนี้มีชีวิตอยู่เมื่อประมาณ 290 ปีก่อนคริสตกาล (ราว พ.ศ. 253) ในนครเซอราคิวส์ (Syracuse) อันเป็นนครรัฐใหญ่แห่งหนึ่งแถบซิซิลี และมีความสนิทสนมกับกษัตริย์ไฮเออโรที่ 2 ความปราดเปรื่องของอาร์คิมีดิสมีมากมาย ทั้งยังมีบทบาทสำคัญในการป้องกัน การโจมตีจากพวกโรมันเมื่อ 213 ปีก่อนคริสตกาล โดยการสร้างยุทโธปกรณ์บางอย่าง แต่เซอราคิวส์ก็ถูกโรมันโจมตีได้ในที่สุด และอาร์คิมีดิสก็เสียชีวิตในคราวนี้ด้วย

อาร์คีมิดิสลงในอ่างอาบน้ำก็เห็นร่างกาย แทนที่น้ำในอ่าง และน้ำก็ล้นออก ทำให้สามารถนำหลักการนี้ ไปใช้พิสูจน์มงกุฎของพระราชาไฮเออโรได้ว่า ช่างทองซื่อตรงหรือไม่

นอกจากนี้ อาร์คิมีดิสยังได้สร้างทรงกลมไว้สองลูก (เล่ากันว่า แม่ทัพโรมัน ได้นำกลับไปโรมด้วย) ลูกหนึ่งเป็นแผนที่ดาว (คล้ายลูกโลก แต่เป็นแผนที่ดาว บนทรงกลมแทน) อีกลูกเข้าใจว่าเป็นแบบจำลองการโคจรของดวงอาทิตย์ ดวงจันทร์ และดาวเคราะห์อื่นๆ สำหรับเรื่องที่ว่าอาร์คิมีดิสเป็นผู้พิสูจน์น้ำหนักของมงกุฎ พระราชานั้น น่าจะเป็นความจริง แต่ที่เล่าว่า พอคิดออกก็ลุกจากโรงอาบน้ำทั้งยัง เปลือยกายล่อนจ้อน แล้วร้อง ยูเรก้า (ความจริงท่านร้องว่า อิว-เรคา [Heureka, Eureka] หมายถึง ฉันพบแล้ว) นั้น คงจะแต่งเล่นในภายหลังมากกว่า

ส่วนการพิสูจน์มงกุฎนั้น ทำโดยนำทองคำบริสุทธิ์ตามน้ำหนักที่กำหนด ไปตวงหาปริมาตร คือ ใส่ในภาชนะปริ่มน้ำ แล้ววัดปริมาตรน้ำที่ล้นออก น้ำล้นจะมีปริมาตรเท่ากับปริมาตรทองคำ หากมงกุฎนั้นเป็นทองบริสุทธิ์ เมื่อใส่อ่างน้ำ ปริมาตรน้ำล้นจะต้องเท่ากับที่วัดจากทองบริสุทธิ์ แต่หากมงกุฎนั้น เป็นทองผสม (โดยช่างทำมงกุฏให้มีน้ำหนักเท่ากับที่กำหนด แต่ความจริง ผสมโลหะอื่นลงไป และลดเนื้อทองให้น้อยลง หากโลหะผสมไม่มากนัก ก็จะแยกแยะด้วยตาเปล่าไม่ออก) ปริมาตรจะมากกว่า เพราะโลหะที่นำมาผสมได้ เช่น เงิน หรือ ทองแดง ล้วนมีความหนาแน่นน้อยกว่าทองคำ หากจะผสมให้มี น้ำหนักเท่าที่กำหนด ต้องเพิ่มโลหะเข้าไปมาก (ความหนาแน่น = น้ำหนักต่อปริมาตร) ความจริงเรื่องเล่าข่าวลือเกี่ยวกับอาร์คิมีดิสยังมีอีกมาก บ้างก็ว่าท่านสามารถ ใช้กระจกเงาจำนวนมหาศาลสะท้อนแสงไปเผาทัพเรือพวกโรมันได้ และยังบอกว่า อาร์คิมีดิสเคยกล่าวว่า “หาที่ให้ฉันยืนสิ ฉันจะงัดโลกให้ดู” นี่ก็เหลวไหลอีกเช่นกัน และยังมีเรื่องเล่าว่า ที่อาร์คิมีดิสถูกทหารโรมันฆ่าตายก็เพราะไม่ยอมมอบแผนผัง ทางคณิตศาสตร์บางอย่างให้

ผลงาน

ผลงานของอาร์คิมีดิสที่เขียนไว้เป็นภาษากรีก มีด้วยกัน 9 เล่ม ดังนี้

ว่าด้วยทรงกลมและทรงกระบอก (On the Sphere and Cylinder) (สองเล่ม) โดยกล่าวว่า พื้นที่ของผิวทรงกลมใดๆ มีค่าเป็น 4 เท่าของพื้นที่วงกลมที่ใหญ่ที่สุด ที่บรรจุในทรงกลมนั้น (สมการในปัจจุบันก็คือ S = 4 r2) และปริมาตรของทรงกลมเป็น 2/3 เท่าของปริมาตรทรงกระบอกที่สูงเท่ากัน (นั่นคือ V = 4/3r3) อาร์คิมีดิสภาคภูมิใจ กับการค้นพบความจริงดังกล่าวมาก และได้ให้จารึกคำสอนดังกล่าวไว้บนหลุมศพของตน โดยทำเป็นรูปทรงกลมบรรจุอยู่ในกระบอก หลังจากอาร์คิมีดิสเสียชีวิตได้ประมาณ 150 ปี ซิเซอโร นักปราชญ์ชาวกรีกผู้มีชื่อเสียงจึงได้พบหลุมศพดังกล่าวซึ่งมีหญ้าขึ้นปกคลุมไปหมด

การวัดวงกลม (Measurement of the Circle) เป็นงานชิ้นสั้นๆ ที่กล่าวถึงอัตราส่วนของค่าพาย () ซึ่งเป็นอัตราส่วนของ เส้นรอบวงกลม ต่อรัศมีของวงกลม ว่ามีค่าอยู่ระหว่างกรอบ 3 1/7 – 3 10/71 ผู้ที่เสนอปัญหานี้คงจะเป็นอาร์คิมีดิส โดยใช้รูปทรงหลายเหลี่ยม เพื่อหาค่า จนมีการพัฒนาเรื่องอนุกรมขึ้นในปลายศตวรรษที่ 17 ผลงานชิ้นนี้ยังแสดง ค่าประมาณที่แม่นยำของรากที่สองของ 3 และของตัวเลขจำนวนมากๆ อีกหลายจำนวน

ว่าด้วยทรงกรวย และทรงกลม (On Conoids and Spheroids) เกี่ยวกับการพิจารณาปริมาตรของเสี้ยวทรงตัน ที่เกิดจากการหมุนภาคตัดกรวย (วงกลม วงรี พาราโบลา หรือ ไฮเพอร์โบลา) รอบแกนของตัวเอง ปัจจุบันนี้เราถือว่านี่เป็นปัญหาการใช้อินทีเกรชั่น สำหรับเรื่อง ว่าด้วยเส้นเกลียว (On Spirals) นั้นได้บรรยายถึงโลคัสของจุดที่เคลื่อนที่ (ด้วยความเร็วคงที่)ไปตามแนวเส้นตรง (ที่กำลังหมุนรอบตัวเองอยู่ด้วยความเร็วคงที่) ณ จุดใดๆ

ว่าด้วยดุลยภาพของระนาบ (On the Equilibrium of Planes) (หรือ จุดศูนย์ถ่วงของระนาบ (Centers of Gravity of Planes) สองเล่ม) ส่วนใหญ่กล่าวถึงการเสนอให้ศูนย์กลางของแรงโน้มถ่วงของระนาบตรงใดๆ เล่มแรกกล่าวถึงกฎของคาน (ระดับความสูงบนคานที่ระยะไกลจากจุดหมุน เป็นอัตราส่วนผกผันกับน้ำหนัก) และจากผลงานเหล่านี้ทำให้ อาร์คิมีดิสได้รับการยกย่องเป็นผู้วางรากฐานวิชากลศาสตร์ทฤษฎี (Theoretical Mechanics)

เสี้ยวของพาราโบลา (Quadrature of the Parabola) เป็นคำบรรยายเชิงกลศาสตร์ในตอนแรก และจากนั้นก็ใช้วิธีการทางเรขาคณิตแบบเดิม ที่ว่าพื้นที่ของส่วนใดๆ ของพาราโบลา จะเท่ากับ 4/3 ของพื้นที่สามเหลี่ยม ที่มีฐานและความสูงเท่ากับส่วนเสี้ยวนั้น และปัจจุบันนี้ปัญหาดังกล่าวต้องอาศัย อินทีเกรชั่นมาอธิบาย

นักคำนวณทราย (The Sand-Reconer) เป็นตำราแต่งไว้สั้นๆ อธิบายให้คนทั่วไปเข้าใจระบบความคิดเรื่องจำนวนของกรีก โดยแสดงวิธีการนับจำนวนที่มีค่ามากๆ เช่น นับเม็ดทรายที่จะถมจนเต็มจักรวาล อาร์คิมีดิสสร้างระบบที่อิงฐานเลข 100,000,000 (พวกบาบีโลนมีระบบอิงฐานเลข 60) นับว่าเป็นตำราที่น่าสนใจมาก เพราะได้พิจารณาเส้นผ่านศูนย์กลางของพระอาทิตย์ ที่ปรากฏ โดยการสังเกตด้วยเครื่องมือ

วิธีการอันเกี่ยวกับทฤษฎีบทกลศาสตร์ (Method Concerning Mechanical Theorems) บรรยายถึงกระบวนการค้นพบในทางคณิตศาสตร์ โดยเล่าถึงการใช้วิธีการเชิงกลศาสตร์ในการค้นพบคำตอบต่างๆ เช่น พื้นที่ของเสี้ยวพาราโบลา รวมทั้งพื้นที่ผิวและปริมาตรของทรงกลม นับเป็นงานชิ้นหนึ่งในบรรดาน้อยชิ้นที่กล่าวถึงเรื่องดังกล่าว และเป็นผลงาน สมบูรณ์ชิ้นเดียวที่หลงเหลือจากสมัยโบราณ

ว่าด้วยเทหวัตถุลอย (On Floating Bodies) (สองเล่ม) พบแต่บางส่วนที่เป็นภาษากรีก ส่วนที่เหลือเป็นเนื้อความที่แปลจากภาษากรีก เป็นภาษาละตินสมัยกลาง นับเป็นงานชิ้นแรกที่ว่าด้วยเรื่องไฮโดรสแตติกส์ และนักวิชาการยกย่องให้อาร์คิมีดิสเป็นผู้วางรากฐานวิชานี้ เป้าหมายของเรื่องนี้ ก็เพื่อพิจารณาตำแหน่งที่ของแข็งต่างๆ จะปรากฏ เมื่อลอยอยู่ในของเหลว โดยขึ้นกับรูปร่าง และการแปรเปลี่ยนตามความถ่วงจำเพาะ ในเล่มแรกได้กล่าวถึง หลักทั่วไปไว้หลายอย่าง โดยเฉพาะ (Proposition 7) หลักที่เรียกภายหลังว่า หลักการของอาร์คิมีดิส กล่าวคือ “ของแข็งที่หนาแน่นกว่าของเหลว จะจมอยู่ใต้ของเหลวนั้น และปริมาตรของเหลวที่ถูกแทนที่ เท่ากับปริมาตร ของของแข็งนั้น” เป็นต้น ส่วนเล่มที่สองเป็นการพิจารณาตำแหน่งต่างๆ ของเสถียรภาพที่วัตถุพาราโบลอยด์หมุนเมื่อลอยในของเหลวที่ความถ่วงจำเพาะสูง

ความจริงแล้วอาร์คิมีดิสได้เขียนตำรับตำราไว้มาก แต่ไม่หลงเหลือให้เราได้ศึกษา พบเห็นแต่ที่กล่าวอ้างอิงไว้ในผลงานของนักปราชญ์ท่านอื่นๆ ในสมัยหลังอาร์คิมีดิส ไม่มากนัก เช่น การแก้ปัญหาที่มีตัวแปรที่ไม่ทราบถึง 8 ตัว หรือสี่เหลี่ยมจัตุรัสที่แบ่งเป็น 14 ส่วนเพื่อเล่นเกมบางอย่าง และยังมีงานบางชิ้นปรากฏแปลเป็นภาษาอาหรับไว้ แม้จะไม่ปรากฏชื่ออาร์คิมีดิส ก็เชื่อได้ว่ามีเค้าความคิดของท่านอยู่ชัดเจน

นอกจากนี้อาร์คิมีดิสยังมีชื่อเสียงในฐานะนักดาราศาสตร์อีกด้วย แต่มีผลงานหลงเหลือมาน้อยเหลือเกิน ที่ปรากฏนั้นเป็นหลักฐานอ้างถึงในงานอื่นๆ เสียเป็นส่วนใหญ่ เช่น การระบุระยะทางระหว่างดวงดาวต่างๆ จากโลก ซึ่งปรากฏในทฤษฎีของพิทาโกรัส

นับว่าอาร์คิมีคิสมีอิทธิพลต่องานด้านคณิตศาสตร์ และวิทยาศาสตร์ ในสมัยต่อมาอย่างมาก แต่ก็ไม่ใช่ว่ามีการศึกษาอย่างต่อเนื่อง นับจากสมัยของ อาร์คิมีดิส มีหลักฐานว่ามีการแปลตำราด้านคณิตศาสตร์ของอาร์คิมีดิสเป็น ภาษาอาหรับในศตวรรษที่ 8-9 นั่นเองที่ทำให้มีการศึกษาผลงานเหล่านี้อย่างจริงจัง โดยเฉพาะเรื่องปริมาตรของทรงตันหมุนรอบตัว และผลงานด้านคณิตศาสตร์ ของปราชญ์ชาวอาหรับในต้นสมัยกลางก็ได้รับอิทธิพลจากการศึกษาผลงานของ อาร์คิมีดิสเป็นจำนวนมาก

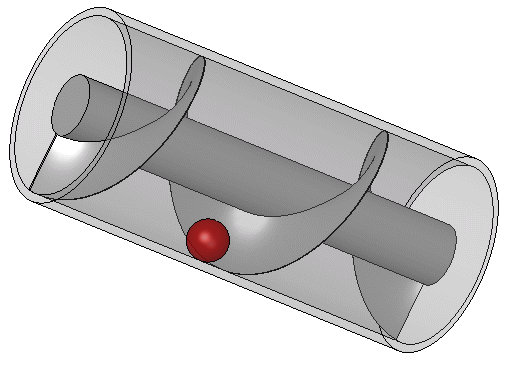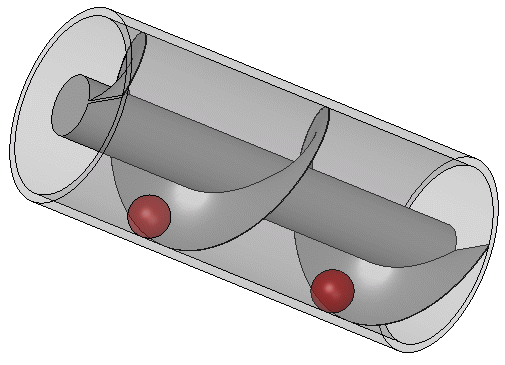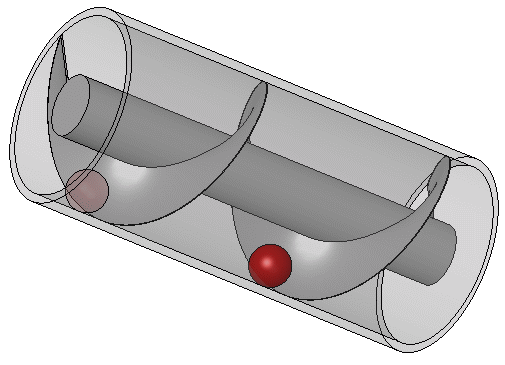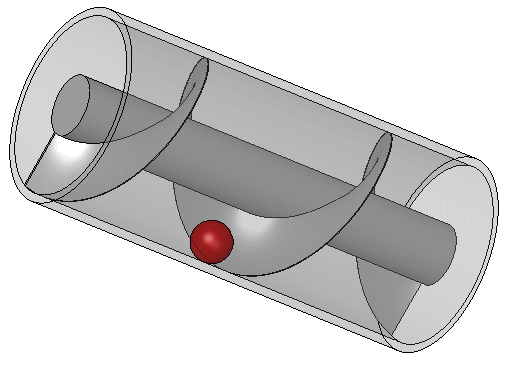
โฉมหน้าของระหัดวิดน้ำแบบอาร์คิมีดิส นอกจากนี้ อาร์คิมีดิสยังได้ชื่อว่า เป็นนักประดิษฐ์ โดยประดิษฐ์อุปกรณ์ที่เรียกว่า ระหัดวิดน้ำแบบอาร์คิมีดิส (Archimedes’s Screw) เป็นเครื่องกลอย่างหนึ่งที่ใช้ชักน้ำจากที่ต่ำขึ้นที่สูงได้ โดยใช้วิดน้ำจากเรือใหญ่ ระหัดแบบนี้ มีโครงสร้างประกบด้วยท่อยาวขดเป็นเกลียว ที่ปลายด้านล่าง มีหอยโข่งปิด และเอียงเป็นมุม 45 องศา ปลายด้านล่างจุ่มลงน้ำ เมื่อเกลียวท่อหมุน น้ำก็จะไหลขึ้นไปตามท่อ ระหัดอาร์คิมีดิสบางแบบใช้หอยโข่งหมุนเวียน รอบท่อซึ่งติดอยู่กับที่ หรือใช้ท่อรูปหอยโข่งหมุนรอบแกนนิ่ง

อย่างไรก็ตาม ผลงานที่มีอิทธิพลมากที่สุดของอาร์คิมีดิสเพิ่งปรากฏ ในศตวรรษที่ 16-17 โดยมีการพิมพ์ตำราภาษากรีก เมื่อ พ.ศ. 2087 ส่วนการแปลเป็นภาษาละตินนั้นมีปรากฏในเวลาหลังจากนั้นไม่นานนัก ซึ่งยังสะท้อนอยู่ในผลงานของนักปราชญ์ผู้มีชื่อเสียงหลายท่าน เช่น เคปเลอร์, กาลิเลโอ เป็นต้น ส่วนฉบับแปลผลงานโดยสมบูรณ์เป็นภาษาละติน รวมทั้งบทอธิบายขยายความของนักปราชญ์โบราณ ก็มีอิทธิพลต่อ นักคณิตศาสตร์ในศตวรรษที่ 17 หลายท่าน โดยเฉพาะ เรเน เดส์คาร์ตส์ และ ปิแอร์ เดอ แฟร์มาต์ กล่าวได้ว่าหากปราศจากพื้นความรู้จากนักคณิตศาสตร์ โบราณที่เพิ่งค้นพบ ใหม่แล้ว พัฒนาการทางคณิตศาสตร์ในยุโรปในสมัย พ.ศ. 1550 – 1650 คงจะบังเกิดขึ้นไม่ได้

โดย…ธวัชชัย ดุลยสุจริต